Unit 6 connecting algebra and geometry through coordinates – In unit 6, the captivating realm of mathematics unveils a profound connection between algebra and geometry, mediated through the enigmatic language of coordinates. This extraordinary union unlocks a world of possibilities, where algebraic equations dance upon the canvas of geometric shapes, and coordinates serve as the bridge that spans these seemingly disparate domains.
Through a captivating narrative, this unit embarks on an exploration of the intricate interplay between algebra and geometry, revealing how coordinates empower us to visualize algebraic concepts and analyze geometric figures with unprecedented clarity. Its applications extend far beyond the classroom, reaching into the practical realms of architecture, engineering, and countless other disciplines.
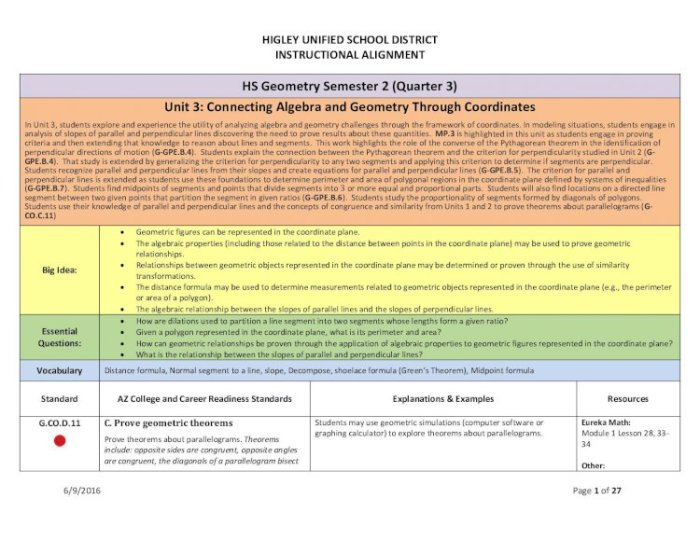
Connecting Algebra and Geometry through Coordinates: Unit 6 Connecting Algebra And Geometry Through Coordinates

The connection between algebra and geometry is strengthened through the use of coordinates. Coordinates provide a way to represent geometric shapes algebraically and to solve geometric problems algebraically.
Understanding the Concept, Unit 6 connecting algebra and geometry through coordinates
Coordinates are ordered pairs of numbers that locate points on a plane. The first number, called the x-coordinate, indicates the horizontal position of the point. The second number, called the y-coordinate, indicates the vertical position of the point. The coordinate plane is a two-dimensional plane that is divided into four quadrants by the x-axis and y-axis.
Algebraic equations can be used to represent geometric shapes. For example, the equation y = x^2 represents a parabola. The equation x + y = 5 represents a line. The equation x^2 + y^2 = 1 represents a circle.
Transforming Algebraic Equations into Geometric Representations
To plot an algebraic equation on the coordinate plane, first solve the equation for y. Then, for each value of x, find the corresponding value of y. Plot the points (x, y) on the coordinate plane.
For example, to plot the equation y = x^2, solve the equation for y: y = x^2. Then, for each value of x, find the corresponding value of y. For example, when x = 1, y = 1. When x = 2, y = 4. Plot the points (1, 1) and (2, 4) on the coordinate plane.
Using Coordinates to Analyze Geometric Figures
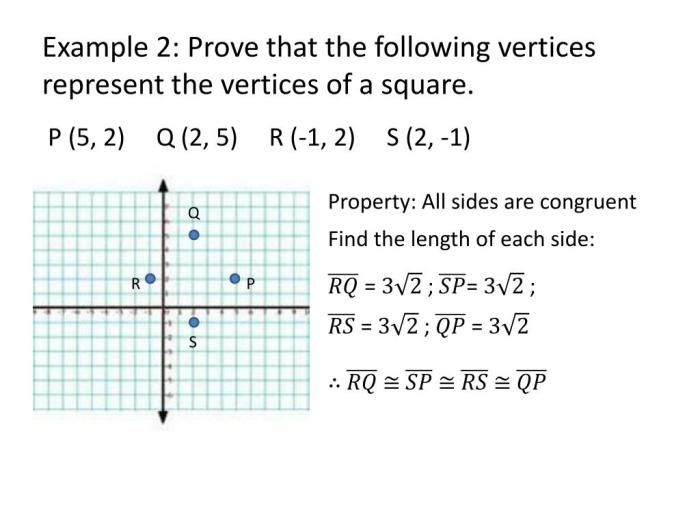
Coordinates can be used to determine the properties of geometric figures. For example, the distance between two points can be calculated using the distance formula: d = sqrt((x2 – x1)^2 + (y2 – y1)^2), where (x1, y1) and (x2, y2) are the coordinates of the two points.
The area of a triangle can be calculated using the area formula: A = (1/2) – base – height, where the base and height are the lengths of the two sides of the triangle that form a right angle.
Applications in Real-World Scenarios
The connection between algebra and geometry through coordinates is applied in various fields, such as architecture, engineering, and computer graphics.
In architecture, coordinates are used to design buildings and other structures. In engineering, coordinates are used to design bridges, roads, and other infrastructure. In computer graphics, coordinates are used to create 3D models and animations.
Quick FAQs
What is the significance of coordinates in connecting algebra and geometry?
Coordinates provide a common language that allows us to represent algebraic equations as geometric shapes and analyze geometric figures using algebraic techniques.
How can we use coordinates to solve geometric problems?
By plotting the coordinates of a geometric figure, we can determine its properties, such as area, perimeter, and angles, using algebraic formulas.
What are some real-world applications of the connection between algebra and geometry through coordinates?
This connection finds applications in architecture, engineering, navigation, and computer graphics, among other fields.